Stability Chapter 1 – Density and relative density Solutions.

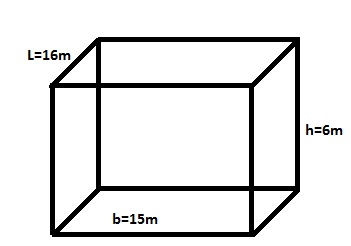
1. A rectangular tank measures 16mx15mx6m. How many tonnes of oil of RD 0.78 can it hold?

SOLUTION:

Given : L =16m , B = 15m, H = 6m, RD=0.7

=16x15x6 = 1440m3

We know that : Density = Mass /Volume
0.78 =Mass/1440m³

Hence, Mass =1123.2 tonnes

2. A cylindrical tank of diameter 8m is 10m high.400t of oil of RD 0.9 is poured in to it. Find the ullage, assuming π to be 3.1416.

SOLUTION:

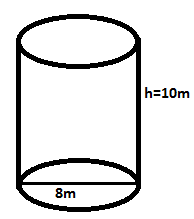
Given: Diameter = 8m,

Radius = (d/2)m
=(8/2)m =4m
Height =10m
Mass = 400t
RD =0.9

We know that: Volume of the cylindrical tank = π²h
= 3.1416 x 4 x 4 x 10
=502.656m³

We know that:
Density = (Mass/Volume)
0.9 = 400/ (Volume of the oil)

Hence, Volume of the oil = 400/0.9
=444.44m³

Depth of oil = volume/area
Area of cylinder   =( π²r)
 =(3.1416 x 4 x 4)
 =502656m³

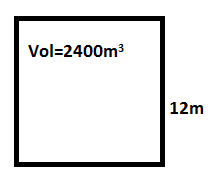
3. A tank of 2400m³ volume and 12 depth, has vertical side and horizontal bottom. Find how many tonnes of oil of RD 0.7 it can hold, allowing 2% of the tank for the expansion .state the ullage of loading.

Solution :-

Given : Volume of the tank = 2400m³
Depth of tank =12m
RD =0.7

According to question 2% of the volume is allowed for expansion.
As we know that

Density = Mass/ Volume
Since volume =(L x B x H)
= 2400m³( given )

So, Area = (volume / depth)
= (2400/12)
=200m²

Mass  =  ( volume x density)
Mass  =  (2400×0.7)
 =1680 t

Since 2% of the volume of the tank allowed for expansion
 = (2/100) x 2400
 = 48m³

Volume of the oil = (volume of the tank – free space )
= ( 2400 -48)
= 2352 m³

Mass of the oil = (volume x density)
 =2352 x 0.7

Depth of oil = (volume of oil /area)
= 2352/(L x B)
= (2352/ 200)
=11.76 m

Hence, Ullage = (12-11.76)
                           = 0.24m.

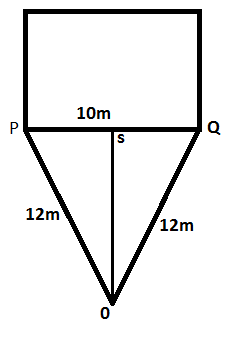
4. A tank 10m deep has vertical sides .its bottom consist of triangle 12mx12mx10m. find the mass of oil (of RD0.800) to be loaded , allowing 3 % of the volume of oil loaded for expansion. State the ullage on completion of loading.

Solution:

Depth of the tank = 10m
L, B, H, of triangle = (12 x 12 x 12
RD = 0.8

Allowing, 3% of the volume of the oil loaded for expansion.
Area of the triangle = 1/2 (base x height)

In triangle PQR, RQ in the height which divide the base at same length.
So In triangle PSR

SR² =PR² –PS²
= (12²– 5²)
= (144 -25)
=119

So, SR = 10.9m
So area of the triangle = 1/2 (10×10.9)
=54.5m²

Volume of the tank = (10 x54.5)
= 545m³

Now, volume of the oil = (Total volume -free space)

let ‘V’ be the volume of the oil
545 = (V + 3/100 x V)
545 = (V + 3V/ 100)
545 = (103V /100)
V = (545 x 100) /103
V = 529.126m³

Mass of the oil = (density x volume)
= 0.8 x 529.126
=423.3 t

Depth of the oil = (volume of oil)/(area)
= (529.126 /54.5)
= 9.7087m

Ullage = ( 10 – 9.708)
                 = 0.292m

5. A rectangular tank measuring 25mx 12m x8m has an ullage pipe projecting 0.3m above the tank top. find the mass of SW in the tank when the ullage is 3.3m.

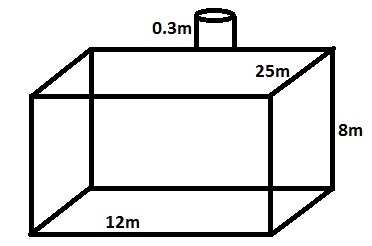
Solution :

Volume of the rectangular tank = ( L x B x H)
= (25 x 12 x 8 )

Pipe above the tank top is 0.3m

Ullage inside the tank = (3.3 – 0.3)
= 3m

Depth of the SW = (8 – 3)
= 5m

Volume of the SW = (L x B x H )
= ( 25 x12 x5)
= 1500 m³

Mass of the SW = (volume x density)
                                 = (1500 x1.025)
                                 = 1537.5 t