Stability 1 – Chapter 5 Effect of Density Solutions

16. A vessel is lying in a river berth of density 1.010 tonnes per m3 , with her summer loadline 20mm above the water on the starboard side and 50mm above the water on the port side . Find how much cargo she can load to bring her to her to her summer loadline in SW, if her summer displacement is 15000 tonnes and TPC is 25.

Solution:

RD of river = 1.010
Summer load line on starboard side = 20mm above
Port side = 50mm above

Mean draft = ( 20 + 50) / 2
= (70/2)
= 3.5cm above

W = 15000t,

FWA = (W/TPC)
= 15000/(40 x 25)
= 15cm

As we know:

Change in draft = 

(Change in RD )x(FWA)
             0.025

= (1.025 – 1.010 ) x 15 / 0.025
= 9cm

Total sinkage  = (9 + 3.5 )
= 12.5cm

TPC = 25( Given)

We know that:

TPC = (A/100) x 1.025
= (25 / 1.025)
= 24.39 m²

Now, TPC for RD 1.010 = (A /100) x( 1.010)
= (24.39 x 1.010)
= 24.63t/cm

Hence ,Cargo can be load = (sinkage x TPC)
= (12.5 x 24.63)
= 307.875 t

17. A vessel is floating in dockwater of RD 1.005with her starboard  WNA  mark 30mm below and her port WNA mark 60mm below the waterline . If her summer SW draught is 8.4m, TPC is 30 and FWA is 160 mm, calculate how much  cargo can be loaded to bring the vessel to her vessel draught in SW.

Solution:

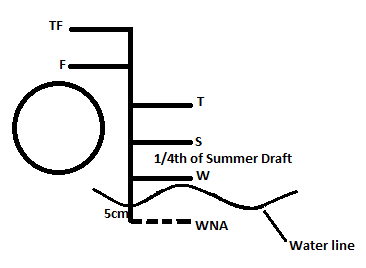
Dockwater  RD = 1.005,
Stbd WNA mark = 30mm below
Port WNA mark = 60mm below
Mean draft = (30 + 60) / 2
= 45mm
=4.5cm,below the water line.

Distance from WNA to water(W) = 50mm
= 5cm

So, sinkage available = (50 – 45)
= 5mm
= 0.5cm

We know that :
Water (W) is 1/48 of summer draft
= (1/48 x 8.4)
= 0.175m
= 17.5cm

Sinkage = (17.5 + 0.5 )
= 18cm

Total sinkage = (18 + 12.8)
= 30.8cm

As we know:

Change in draft = 

(Change in RD )x(FWA)
             0.025

= (1.025 – 1.005 )x 16 / 0.025
= 12.8cm

Again, TPC = (A/100) x density
30 = (A/100) x 1.025
A  =  30/ 1.025
A  = 29.268 m²

Now , TPC for density of 1.005
TPC = (A/100) x 1.005
= (29.268 x 1.005)
= 29.41  t/cm.

Hence ,cargo can be loaded = (30.8 x 29.41)
= 905.82 t

18. A vessel is loading in a SW dock and is lying with her starboard winter loadline 60mm above and her port winter loadline 20mm below the surface of water. if her summer draught in SW is 7.2m and TPC is 20,, find how many tonnes of cargo the vessel can load to bring to her  down to her tropical loadline in SW.

Solution:

Starboard winter load line  = 60mm above
Port winter load line = 20mm below
Mean draft = ( 60 – 20)/2
= (40/2)
= 20mm
= 2cm

Summer SW draft = 7.2m( given)

We know that:

Waterline (W) = (1/48 of summer draft)
=(1/48 x 7.2)
= 0.15m
= 15cm

Total sinkage available to bring the vessel to her tropical load  line  = ( 2+ 15 + 15)
= 32cm

TPC =20( given)
So, Cargo can be load = (TPC x sinkage)
=(20 x 32)
= 640t.

19. From the following details, Calculate the DWT available :- present free board: port 3.0m, starboard 2.9m in water of RD 1.020 FWA 200mm. TPC 30. Statutory summer free board 2.8m.

Solution :

For, Port Side = (3 -2.8)  = 0.2m
= 20cm (above )

For , Starboard side =( 2.9 – 2.8) =0. 1m
= 10cm above

Hence ,Mean freeboard can be calculated as
= (20+ 10)/2
= 30 /2 cm
= 15cm available

As we know:

Change in draft = 

(Change in RD )x(FWA)
             0.025

= (1.025 – 1.020 ) x 20 /0 .025
= 4cm

Now, Total sinkage = (15 + 4)cm
= 19cm

TPC = 30( given)
TPC   =  (A/ 100) x density
30   = (A/100) x 1.025
A = 30/ 1.025
= 29.268m²

Again for calculating  ,TPC at RD 1.020
= (A/100) x ( 1.020)
=  29.85 t/cm

Now , Cargo can be load =( TPC x sinkage)
= (29.85 x 19)
= 567.15 t

20. From the following information , calculate the DWT available up to the tropical loadline SW :-

Persent freeboards : port 1.6m, starboard 1.79m inRD 1.017.
Tropical SW freeboard : 1.63m
Tropical of  SW draft : 9.6m
FWA 150mm, TPC 20.4 .

Solution :

Present freeboard port = 1.68cm
Stbd side = 1.79m
Water of RD = 1.017,
Tropical SW freeboard = 1.63c
Tropical SW draft = 9.6m
FWA = 150mm
TPC = 20.4